专业高效
微纳加工公司

作者：

• Ben King*

• Hans Wenzel

• Eduard Kuhn

• Mindaugas Radziunas

• Paul Crump

机构：

1. 弗迪南德-布劳恩研究所（FBH），德国柏林，Gustav-Kirchhoff-Str. 4, 12489

2. 魏尔斯特拉斯应用分析与随机研究所（WIAS），德国柏林，Mohrenstraβe 39, 10117

联系邮箱：
ben.king@fbh-berlin.de

摘要：
我们报告了一种光子晶体面发射激光器（PCSEL）的设计，该激光器采用全半导体（InGaP/GaAs）光子晶体，适用于超大面积发射和高功率运行。利用PCSEL的耦合波理论，我们对无限和有限尺寸腔的PCSEL进行了建模，结果表明，具有方形晶格周期性并旋转拉伸三角形特征的光子晶体单元设计适合实现超大面积（正方形腔的尺寸为1 mm<L<3 mm1 \, \text{mm} < L < 3 \, \text{mm}1mm<L<3mm 的L×LL \times LL×L ）的PCSEL，同时保持了基模激光模式与高阶腔模式之间的高模式区分度以及高外部效率。这一目标通过采用一种单晶格光子晶体单元设计实现，该设计最小化了光子晶体中的一维耦合，为双晶格PCSEL提供了一种有前景的替代方案。

划重点：

我们为客户提供晶圆（硅晶圆，玻璃晶圆，SOI晶圆，GaAs，蓝宝石，碳化硅（导电非绝缘），金刚石，GaN（外延片/衬底）），镀膜方式（PVD,cvd,Ald，PLD）和材料（Au Cu Ag Pt Al Cr Ti Ni Sio2 Tio2 Ti3O5，Ta2O5,ZrO2,TiN，ALN,ZnO,HfO2。。更多材料），键合（石英石英键合，蓝宝石蓝宝石键合）光刻，高精度掩模版，外延，掺杂,电子束直写等产品及加工服务(请找小编领取我们晶圆标品库存列表，为您的科学实验加速。

EBL代工（非晶硅，TiO2,SiO2,GaN，Ta2O5，Al,Au,GaAs/GaN(PCSEL)...更多材料体系）,母版制作，铬版销售，纳米压印，DUV光刻超结构服务，

请联系小编免费获取原文，也欢迎交流半导体行业，工艺，技术，市场发展！

1. 引言
光子晶体面发射激光器（PCSELs）是一类半导体激光器，它利用二维光子晶体在激光器平面内提供大面积二维分布反馈并实现表面发射耦合 [1]。PCSELs 的一个关键特性是能够将器件扩展至大面积以实现高功率运行，同时保持单模或低模式数运行 [2]。这使得PCSELs有潜力实现发射面积比其他单片单模激光二极管更大的单模激光器。最近，实验表明，具有3毫米直径圆形腔的PCSEL能够实现50 W连续波功率，并产生约0.05°发散的圆形光束 [3]。研究还表明，通过进一步扩展单个器件的尺寸，可以实现kW级单模连续波输出功率 [4]。如果此类超大面积PCSELs能够以一致性、高产量、低成本以及高可靠性和功率转换效率制造出来，它们有潜力在高亮度应用中超越所有其他激光二极管，并直接与固态激光器和光纤激光器竞争。

现有文献中报道的所有高功率PCSELs均采用高对比度的孔/半导体方形晶格光子晶体 [3,5–9]，其中通过刻蚀和外延再生长形成的孔洞与半导体之间提供折射率对比。然而，目前尚不清楚在再生长过程中引入孔洞究竟如何影响PCSELs的可靠性、功率转换效率或大规模可制造性。尤其是，关于高功率GaAs PCSELs的电压和功率转换效率的报告较少。在2020年，一种在室温连续波（CW）工作条件下实现约12.5%功率转换效率的PCSEL被报道，其输出功率为5 W [10]。通过提高斜率效率，一条达到约35%效率的路径被提出，并在随后的50 W器件中部分实现 [3]，但这一效率显著低于最佳边发射器 [11] 和 VCSELs [12] 的效率水平。

全半导体PCSELs被提出 [13,14]，其中光子晶体中的折射率对比由两种半导体材料提供，这类似于再生长光栅技术成熟的分布反馈激光器（DFB），在效率或电阻方面几乎无损失 [15,16]。尽管实验上已实现全半导体PCSELs [17–19]，但仅限于小尺寸器件，并且报告的输出功率和转换效率较低。此外，这些器件尚未证明能够在大面积二维模式下运行。实际上，有研究表明，由于与空气孔相比折射率对比较低，全半导体PCSELs最终可能因二维耦合弱而不可行 [2]。

在本研究中，我们提出了一种基于GaAs的PCSEL，其采用全半导体InGaP/GaAs光子晶体设计，工作波长为1070 nm，适用于超大面积和高功率运行。利用基于PCSELs耦合波理论的工具 [20–22]，我们对无限和有限尺寸的PCSELs进行了建模，证明采用方形晶格光子晶体和旋转拉伸三角形特征的全半导体PCSEL可以在方形腔尺寸为1 mm<L<3 mm1 \, \text{mm} < L < 3 \, \text{mm}1mm<L<3mm 的超大面积PCSEL中提供与最优孔洞设计相当的模式区分能力，同时保持较高的外部效率。

我们展示了一个优化全半导体PCSEL的计算示例，其中L=2 mmL = 2 \, \text{mm}L=2mm，其基模与二阶腔模之间的增益区分为2.6 cm−1^{-1}−1，并具有窄的圆形远场分布。此外，我们还展示了将腔长扩展至L=5 mmL = 5 \, \text{mm}L=5mm 的路径，同时在基模与高阶腔模之间维持合理的模式区分。如此大面积的器件可能使单孔径高亮度光束中实现10 W甚至100 W以上的连续波功率成为可能 [4]，尤其是在全半导体技术降低材料损耗的情况下。

2. 方法

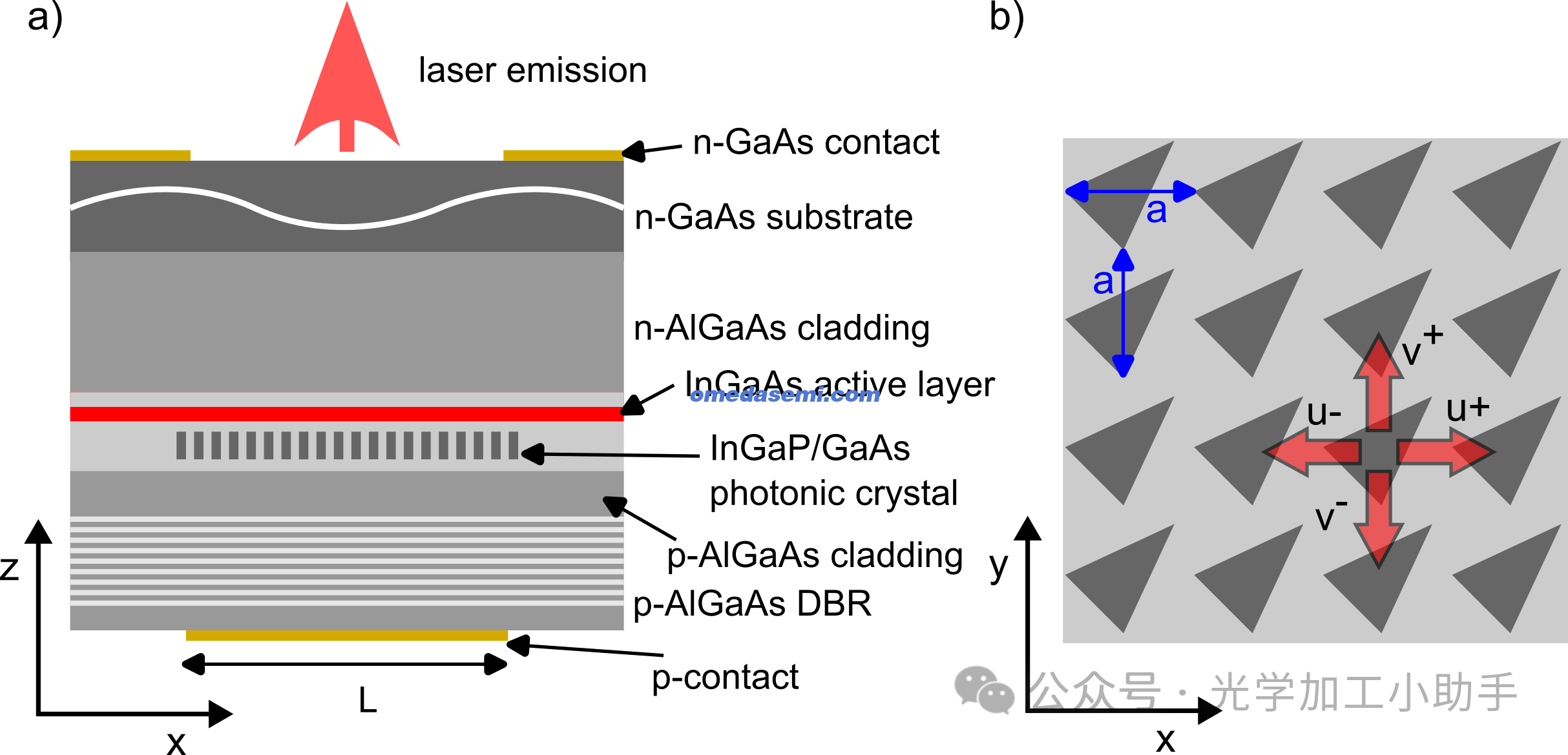
为了设计我们的PCSEL结构，我们采用了基于耦合波理论的数值模型，该模型用于模拟方形晶格、横向电（TE）极化的PCSEL [20–24]。我们未考虑时间相关效应，例如载流子效应或加热效应。在PCSEL的耦合波理论中，我们研究了在光子带结构Γ点处结构中沿横向xxx 和yyy 方向传播的四个基本波的相互作用，如图1(b)所示：

Ψ=(u+(x,y)u−(x,y)v+(x,y)v−(x,y))Ψ = \begin{pmatrix} u^+(x, y) \\ u^-(x, y) \\ v^+(x, y) \\ v^-(x, y) \end{pmatrix}Ψ=u+(x,y)u−(x,y)v+(x,y)v−(x,y)

这些基本波在x−yx-yx−y 平面中通过光子晶体实现二维耦合，同时在zzz 方向上耦合以实现表面发射。这四个基本波的耦合由一个4×44 \times 44×4 的矩阵CCC 表示，该矩阵包含了光子晶体在xxx 和yyy 方向的设计效果，以及在zzz 方向上垂直外延结构的设计，包括内部和外部材料界面的反射效果。参考文献 [4] 表明，矩阵CCC 可以写为：

C=CHermitian+Cnon-HermitianC = C_{\text{Hermitian}} + C_{\text{non-Hermitian}}C=CHermitian+Cnon-Hermitian

其中，Cnon-HermitianC_{\text{non-Hermitian}}Cnon-Hermitian 表示器件中的非厄米耦合，它对器件的表面辐射起作用，而CHermitianC_{\text{Hermitian}}CHermitian 表示平面内的厄米耦合。对于y=xy = xy=x 的晶格单元对称性，CHermitianC_{\text{Hermitian}}CHermitian 可表示为 [4]：

CHermitian=(κ11κ1Dκ2D+κ2D−κ1D∗κ11κ2D−∗−κ2D+κ2D+κ2D−κ11κ1Dκ2D−∗−κ2D+κ1D∗κ11)C_{\text{Hermitian}} = \begin{pmatrix} κ_{11} & κ_{1D} & κ_{2D+} & κ_{2D-} \\ κ_{1D}^* & κ_{11} & κ_{2D-}^* & -κ_{2D+} \\ κ_{2D+} & κ_{2D-} & κ_{11} & κ_{1D} \\ κ_{2D-}^* & -κ_{2D+} & κ_{1D}^* & κ_{11} \end{pmatrix}CHermitian=κ11κ1D∗κ2D+κ2D−∗κ1Dκ11κ2D−−κ2D+κ2D+κ2D−∗κ11κ1D∗κ2D−−κ2D+κ1Dκ11

其中，κ1Dκ_{1D}κ1D 表示反向传播波之间的1D耦合，κ2D+κ_{2D+}κ2D+ 和κ2D−κ_{2D-}κ2D− 表示正交传播波之间的2D耦合，而κ11κ_{11}κ11 表示自耦合。κ11κ_{11}κ11 和κ2D+κ_{2D+}κ2D+ 是实数，而κ1Dκ_{1D}κ1D 和κ2D−κ_{2D-}κ2D− 是复数。

矩阵Cnon-HermitianC_{\text{non-Hermitian}}Cnon-Hermitian 表示为：

Cnon-Hermitian=(iμiμeiθpc00iμe−iθpciμ0000iμiμeiθpc00iμe−iθpciμ)C_{\text{non-Hermitian}} = \begin{pmatrix} i\mu & i\mu e^{iθ_{pc}} & 0 & 0 \\ i\mu e^{-iθ_{pc}} & i\mu & 0 & 0 \\ 0 & 0 & i\mu & i\mu e^{iθ_{pc}} \\ 0 & 0 & i\mu e^{-iθ_{pc}} & i\mu \end{pmatrix}Cnon-Hermitian=iμiμe−iθpc00iμeiθpciμ0000iμiμe−iθpc00iμeiθpciμ

其中，iμi\muiμ 是一个表示通过辐射波进行的自耦合的虚数，iμe±iθpci\mu e^{\pm iθ_{pc}}iμe±iθpc 表示通过辐射波进行的反向传播波之间的1D耦合，θpcθ_{pc}θpc 是由晶格单元几何结构定义的相位项 [4]。

在本文中考虑的方形晶格TE极化PCSEL中，2D耦合仅通过光子晶体中的高阶波发生，而1D耦合通过直接耦合、辐射波耦合以及高阶波耦合共同发生 [23]。需要求解的谱特征值问题为：

ΩΨ(x,y)=CΨ(x,y)+i(∂∂xu+−∂∂xu−∂∂yv+−∂∂yv−)\Omega Ψ(x, y) = CΨ(x, y) + i \begin{pmatrix} \frac{\partial}{\partial x}u^+ - \frac{\partial}{\partial x}u^- \\ \frac{\partial}{\partial y}v^+ - \frac{\partial}{\partial y}v^- \end{pmatrix}ΩΨ(x,y)=CΨ(x,y)+i(∂x∂u+−∂x∂u−∂y∂v+−∂y∂v−)

特征值的实部对应于模式相对于布拉格频率的频率偏移，表示为ℜ(Ω)vg\Re(\Omega)v_gℜ(Ω)vg，其中vgv_gvg 是群速度；虚部对应于总光学损耗，表示为g=2ℑ(Ω)g = 2\Im(\Omega)g=2ℑ(Ω)。在本研究中，为了简化分析，我们未考虑结构中的内部材料损耗，例如波导或基板中的吸收损耗或散射损耗，因此ggg 是由器件两个表面以及平面内边缘的总辐射损耗。我们定义器件中的基模区分度为：

Δg=g1−g0\Delta g = g_1 - g_0Δg=g1−g0

其中，g0g_0g0 和g1g_1g1 分别表示最低损耗（基模）模式和第二低损耗（第一个高阶模式）的总模式损耗。

在 3.1 节 中，我们首先考虑无限腔尺寸的PCSEL，在这种情况下，Ψ\PsiΨ 不随空间变化，因此方程 (5) 的最后一项为零。求解谱问题得到了对应于光子带结构Γ点光子带边的四个解，我们按频率升序分别标记为模式 A、B、C 和 D，其中ggg 是每种模式的总辐射表面损耗。

在 3.2 节 中，我们将分析扩展到有限腔PCSEL，考虑具有尺寸为L×LL \times LL×L 的正方形腔的器件，该腔使用20×2020 \times 2020×20 的均匀数值网格进行离散化，并假设边界条件为：

u+(0,y)=u−(L,y)=v+(x,0)=v−(x,L)=0u^+(0, y) = u^-(L, y) = v^+(x, 0) = v^-(x, L) = 0u+(0,y)=u−(L,y)=v+(x,0)=v−(x,L)=0

正如参考文献 [20] 中所讨论的，即使对于大LLL 的PCSEL，较粗的数值网格和高精度阶数方案也足以对主要模式进行良好逼近。

腔内通过受激发射产生的总光功率表示为PstimP_{\text{stim}}Pstim。由于在本研究中未考虑内部材料损耗（如吸收或散射），光功率仅通过辐射从器件中损失。这包括从器件 p 面表面辐射的功率PsurfaceP_{\text{surface}}Psurface、从器件 n 面基板辐射的功率PsubstrateP_{\text{substrate}}Psubstrate，以及从腔的侧边辐射的功率PedgeP_{\text{edge}}Pedge。我们将PsubstrateP_{\text{substrate}}Psubstrate 视为器件的有用发射。因此，我们为有限腔PCSEL定义以下效率：

ηsubstrate=PsubstratePstim,ηedge=PedgePstim\eta_{\text{substrate}} = \frac{P_{\text{substrate}}}{P_{\text{stim}}}, \quad \eta_{\text{edge}} = \frac{P_{\text{edge}}}{P_{\text{stim}}}ηsubstrate=PstimPsubstrate,ηedge=PstimPedge

其中，ηsubstrate\eta_{\text{substrate}}ηsubstrate 定义了器件基板发射的功率分数，即外部效率；ηedge\eta_{\text{edge}}ηedge 定义了从腔侧边发射的光分数（在实际器件中将被吸收）。我们将ηsubstrate\eta_{\text{substrate}}ηsubstrate 视为器件的外部效率。

关于如何求解无限腔和有限腔大面积器件的谱问题的更多细节，请参见参考文献 [20–22]

图1.
(a) 典型的基板发射型PCSEL的垂直截面示意图，带有 p 面分布式布拉格反射器（DBR）。
(b) 方形晶格光子晶体的示意图，其周期为aaa，红色箭头表示结构中基本波的传播方向。

3. 结果

3.1. 单元晶格与垂直结构

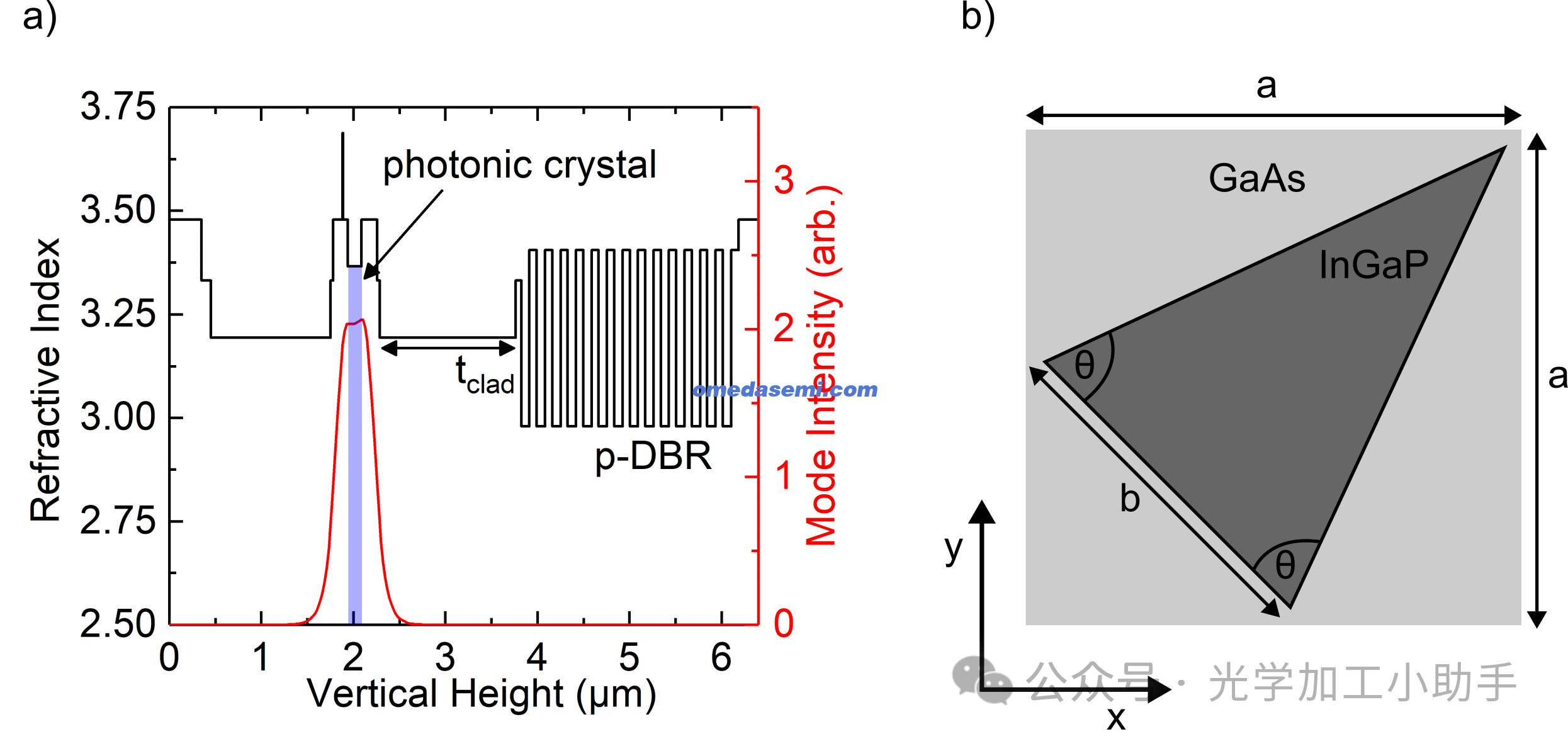
本文研究的垂直外延层结构如图2(a)和表1所示。该结构包含一个用于在λ=1070 nm\lambda = 1070 \, \text{nm}λ=1070nm 发射的单层 InGaAs 量子阱，嵌入在 GaAs 波导中。光子晶体层由嵌入激光器 p-GaAs 波导中的 InGaP/GaAs 光子晶体组成，可通过两步外延生长工艺实现，并伴随中间的干法刻蚀步骤。在 GaAs 材料系统中，可以实现更大的折射率对比，最大对比度可在 GaAs 和 AlAs 之间实现。光子晶体的高度为 150 nm，晶格周期约为a=320 nma = 320 \, \text{nm}a=320nm。

我们研究的光子晶体单元具有方形晶格周期性，并包含一个等腰三角形特征，三角形旋转至具有y=xy = xy=x 对称性，内部角为θ\thetaθ，底边长度为bbb。三角形区域由 InGaP 构成，而三角形外部由 GaAs 构成。单元晶格的示意图如图2(b)所示。

我们的PCSEL设计为从基板发射光，利用 p-DBR（分布式布拉格反射器）回收向器件顶部 p 面耦合的光。

图2.
(a) 本文研究的外延结构的折射率分布与垂直模式强度分布，作为垂直高度的函数。光子晶体层（以蓝色表示）以平均折射率表示（其中单元晶格的39%为InGaP）。
(b) 本文研究的光子晶体单元晶格的示意图，其中三角形的底边长度bbb 和内角θ\thetaθ 为需优化的参数。

表1. 本工作中考虑的外延层结构

3.2 无限腔体PCSEL

我们首先考虑一个无限腔体尺寸的PCSEL（光子晶体表面发射激光器）。在优化我们的无限腔体光子晶体单元时，我们的设计目标包括以下三个点：

设计点（DP）：

• **DP.1：**最低损耗带边模式具有足够的辐射损耗。

• **DP.2：**最低损耗和次低损耗带边模式之间具有较大的辐射损耗差异。

• **DP.3：**尽量减少一维平面内耦合强度的幅度。

DP.1 是实现高效激光器的必要条件：外耦损耗必须足够高，以覆盖内部光学损耗以及PCSEL腔体边缘的损耗（在无限腔体PCSEL中不考虑这些边缘损耗）。同时，辐射损耗也不应过高，否则可能导致设备的阈值过高，但在全半导体设备中这通常不是主要问题。我们使用的条件是辐射损耗应大于10 cm⁻¹，与高功率PCSEL的报告值相当。

DP.2 和 DP.3 是实现单模或低模激光（即单波长发射）的条件。DP.2 通过带边模式的表面辐射损耗差异来区分Γ点的四个带边模式。我们选择差异应大于20 cm⁻¹，参照文献[4]的建议。

DP.3 用于在同一光子带内保持基本模式与高阶腔体模式之间的区分。通过减弱平面内的耦合强度，可以增加腔体边缘模式的损耗，这种边缘损耗对高阶腔体模式影响更大。我们特别关注减少一维耦合系数 |κ₁D|，因为对于小折射率对比的PCSEL，一维耦合通常较大。我们优化 |κ₁D| 而不是包括非厄米耦合在内的总一维耦合，以便分别优化垂直出射和结构中的平面内约束。因此，在 DP.3 中，我们的目标是在实现 DP.1 和 DP.2 的前提下最小化 |κ₁D|。

单元设计和结果

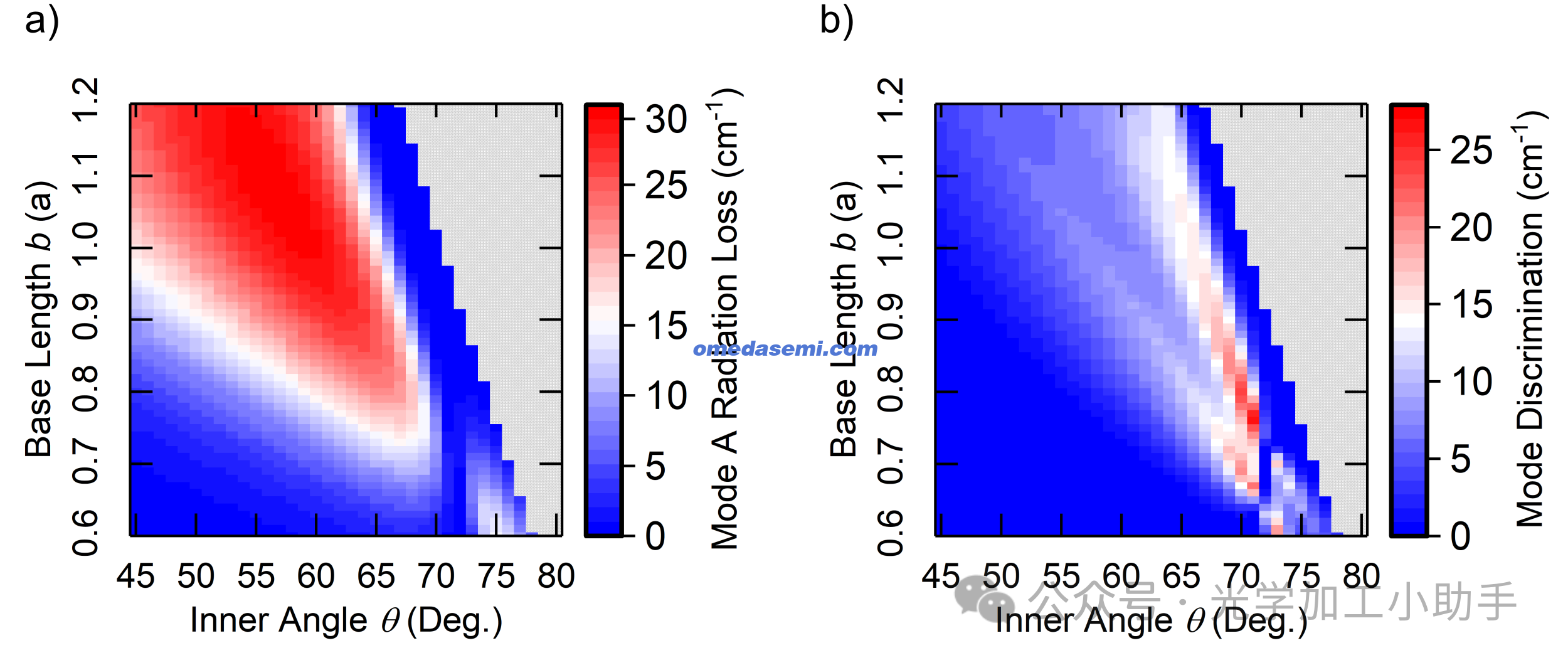
我们对不同单元三角几何进行了参数研究以实现这些设计点。初步结构如图2（a），但不包括p侧布拉格反射镜（DBR），也不考虑外部界面（半导体/空气边界）的垂直反射。我们的目标是模式A（最低频带边模式）作为最低损耗的激射模式。在图3中，我们通过改变单元的θ角和基长b，绘制了：

• (a) 模式A的辐射损耗g。

• (b) 模式A与次低损耗模式之间的损耗差异Δg。

可以看出，总体上我们的全半导体PCSEL可以实现高辐射损耗（g > 30 cm⁻¹）和高模式区分度（Δg > 25 cm⁻¹）。最终选择的设计是θ=70°，基长b=0.75a，其参数为：

• 模式A的辐射损耗：g=8.7 cm⁻¹

• 模式区分度：Δg=16.2 cm⁻¹

• 一维耦合系数：|κ₁D|=51.4 cm⁻¹

包括p侧DBR的影响

我们进一步考虑加入p侧DBR以回收向p侧辐射的光。在图5中，随着p包层厚度（tclad）变化，绘制了：

• (a) 带边模式的辐射损耗g。

• (b) 模式A与次低损耗模式之间的区分度Δg。

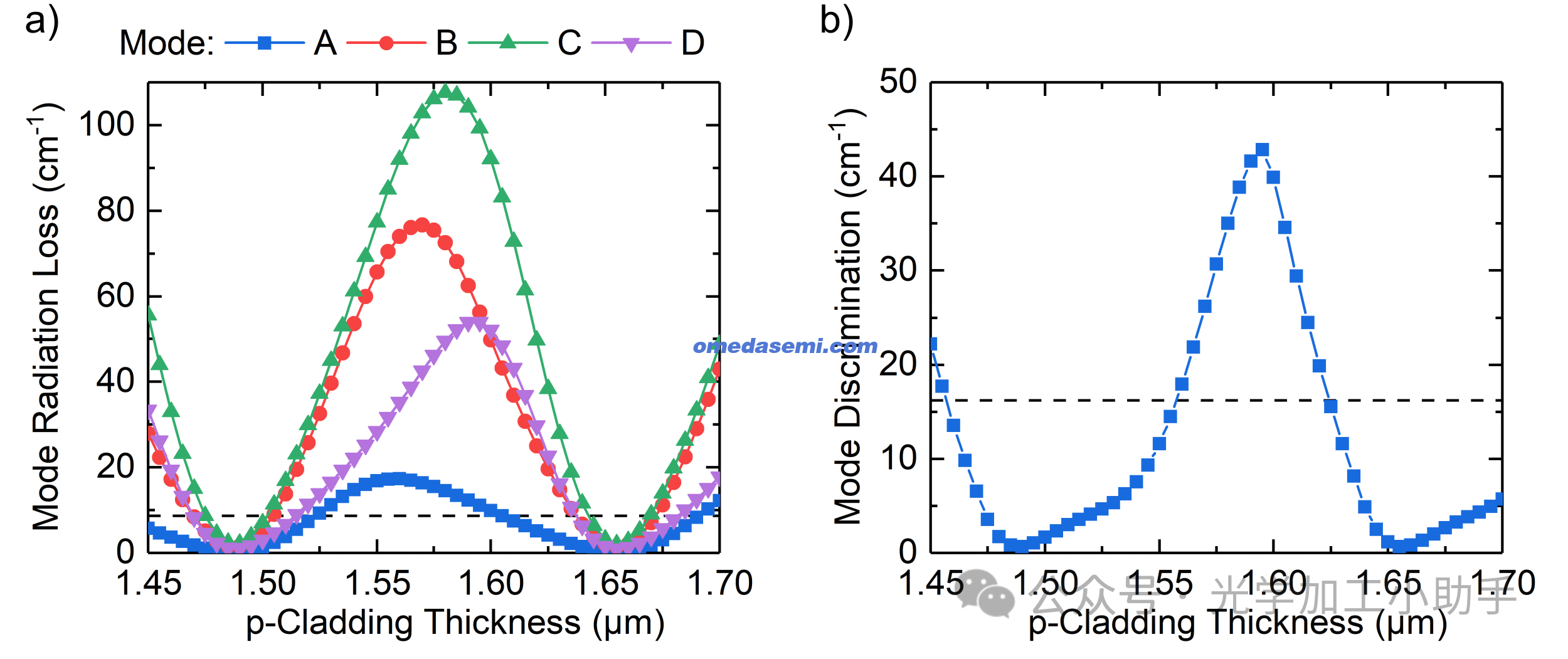
结果表明，通过调整tclad可以控制模式的辐射损耗和区分度。选择tclad=1.565 µm后，模式A的辐射损耗增加到g=17.0 cm⁻¹，模式区分度提高到Δg=21.9 cm⁻¹，从而满足所有设计点。

图3. 光子晶体单元特征的内角 θ 和基长 b 的变化对无限腔体PCSEL的影响

研究了一个无限腔体PCSEL（无p侧DBR和外部表面的反射），通过改变光子晶体单元的内角θ和基长b，绘制了以下内容：

• (a) 最低频模式（模式A）的辐射损耗g。

• (b) 模式A与次低损耗带边模式之间的模式区分度Δg。

灰色区域表示未模拟的单元几何，因为这些区域内的单元特征与相邻单元发生了重叠。

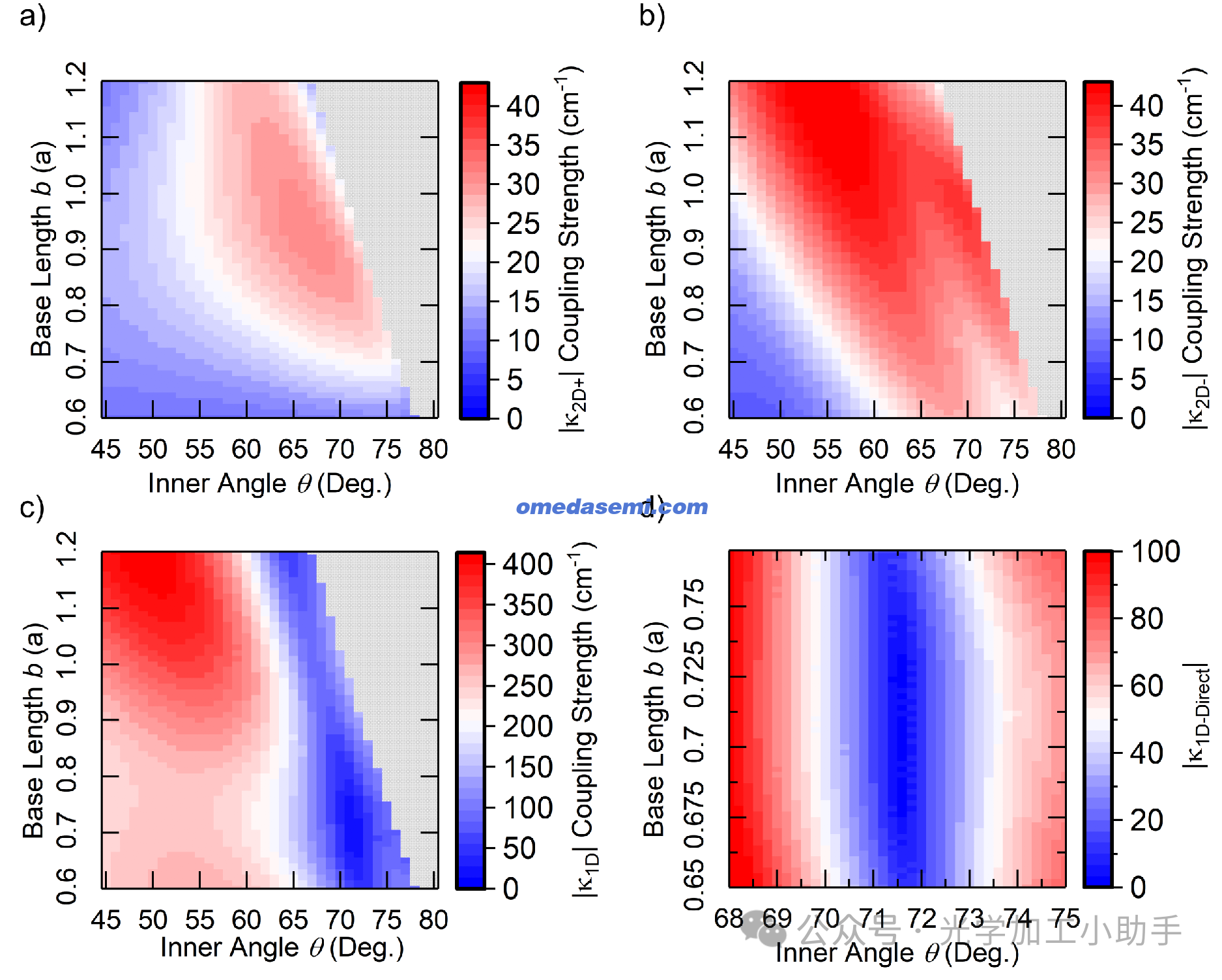
图4. 光子晶体单元特征的内角θ和基长b的变化对无限腔体PCSEL的影响

研究了一个无限腔体PCSEL（无p侧DBR和外部表面反射），通过改变光子晶体单元的三角形特征的内角θ和基长b，绘制了以下内容：

• (a) Hermitian耦合矩阵的元素 |κ₂D⁺|。

• (b) Hermitian耦合矩阵的元素 |κ₂D⁻|。

• (c) Hermitian耦合矩阵的一维耦合系数 |κ₁D|。

• (d) 绘制了 |κ₁D−Direct|，即直接一维耦合对 |κ₁D| 的贡献。

灰色区域表示未模拟的单元几何，因为这些区域内的单元特征与相邻单元发生了重叠。

5. 改变p侧包层厚度tclad对无限腔体PCSEL的影响

研究了一个无限腔体PCSEL，通过改变p侧包层厚度tclad，计算了以下内容：

• (a) 四个带边模式的辐射损耗。

• (b) 最低损耗和次低损耗带边模式之间的模式区分度。

虚线分别表示：

• (a) 在没有p侧DBR的结构中，模式A的辐射损耗。

• (b) 在没有p侧DBR的结构中，模式区分度。

  3.3 有限腔体PCSEL

  我们现在考虑一个长度为L的正方形腔体的有限尺寸PCSEL。我们使用图1和表1中定义的PCSEL结构，其中θ = 70°，b = 0.75 a，tclad = 1.565 µm。

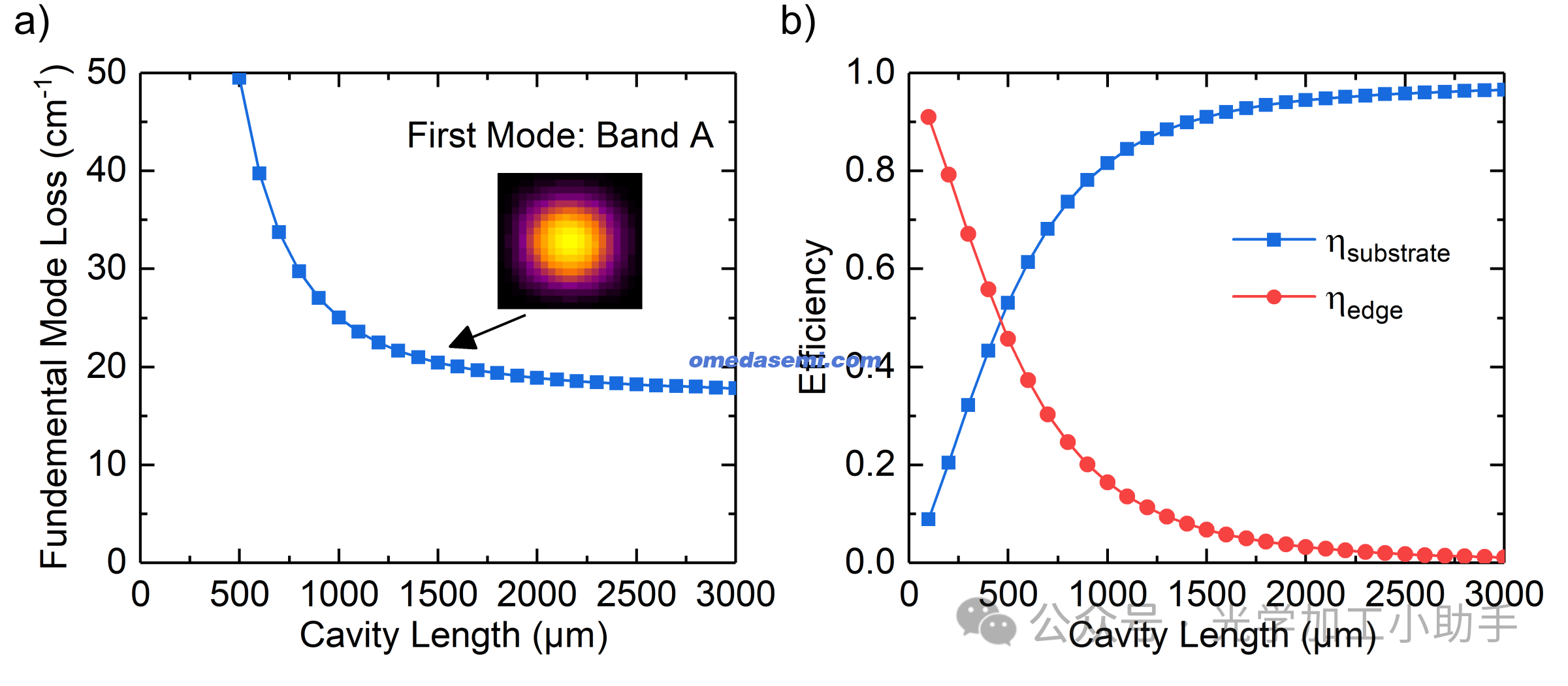
  在图6(a) 中，绘制了最低损耗PCSEL模式的损耗g随L变化的曲线，这对应于A带最低损耗模式。插图展示了L = 1.5 mm时模式的近场分布示例。

  在图6(b) 中，绘制了最低损耗模式的效率ηsubstrate和ηedge。可以看出，随着L增加，g逐渐减小并最终在高L时趋于饱和。从外部效率来看，这种趋势是由于小L时腔体边缘的高损耗所致，随着腔体尺寸的增加，边缘损耗减小。当高L时损耗饱和，外部效率接近ηsubstrate = 1，表明向器件p侧耦合的光被有效地回收利用。

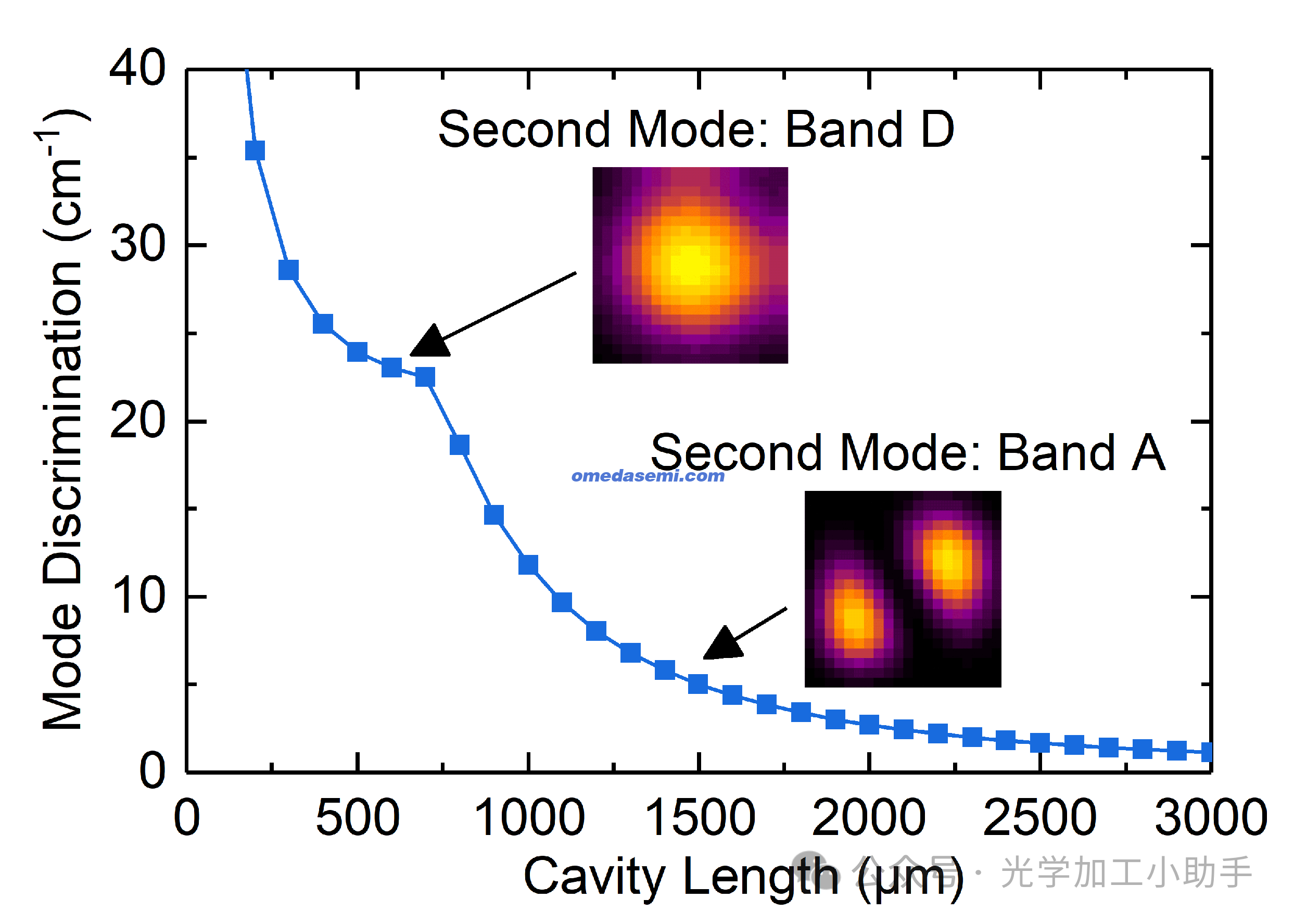
  在图7 中，我们改变L并计算两个最低损耗模式之间的模式区分度Δg。插图展示了第二低损耗模式在L < 700 µm和L > 700 µm时的近场分布示例。在L = 1 mm时，我们实现了非常大的模式区分度Δg ≈ 11.8 cm⁻¹，即使在L = 3 mm时仍保持Δg ≈ 1.1 cm⁻¹，这得益于我们的单元设计最小化了|κ₁D|。可以看出，随着L变化存在两种不同的模式：

  当L < 700 µm时，器件中的第二模式对应于D带的基态带边模式。

  当L > 700 µm时，第二低损耗模式切换为A带的高阶腔体模式，其近场分布呈现双峰结构。

• 

图6. 改变PCSEL腔长L的影响

研究了具有p侧DBR和tclad = 1.565 µm的PCSEL，通过改变腔长L绘制了以下内容：

• (a) 最低损耗模式的总模式损耗g。插图展示了L = 1.5 mm时最低损耗模式的近场分布，使用线性比例的伪彩色图表示。

• (b) 最低损耗模式的效率：ηsubstrate（底部出射效率）和ηedge（边缘效率）。

• 

  
  

  图7. 改变PCSEL腔长L对模式区分度Δg的影响

  研究了具有p侧DBR和tclad = 1.565 µm的PCSEL，通过改变腔长L绘制了两个最低损耗模式之间的模式区分度Δg。

  插图展示了短腔长度区域（D带）和长腔长度区域（A带）中第二低损耗模式的近场分布，使用线性比例的伪彩色图表示。

  

  
  

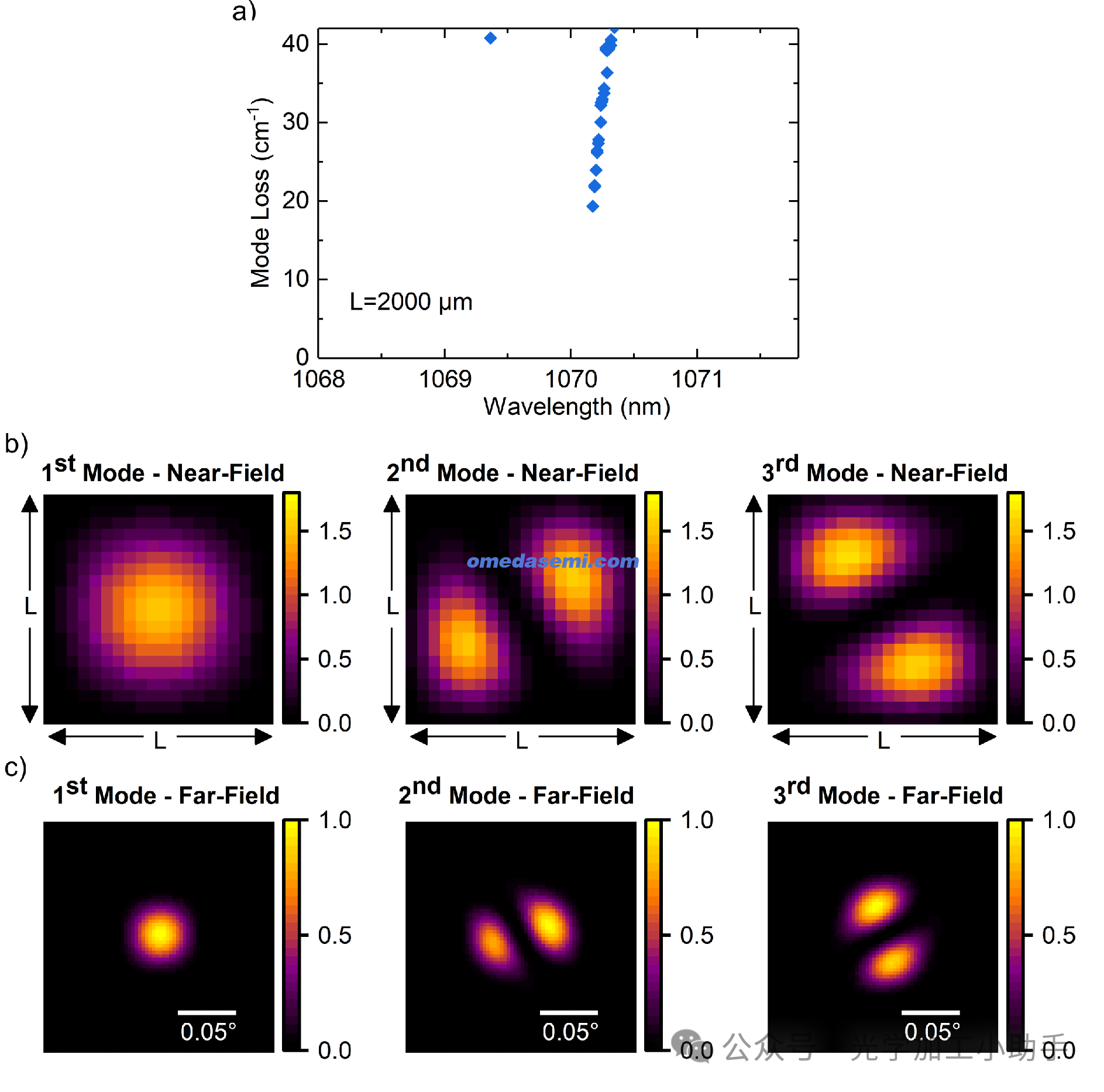
  图8. 对腔长L = 2 mm的PCSEL的模式分析

  对于腔长为L = 2 mm的PCSEL，绘制了以下内容：

• (a) 模式光谱g，表示每个模式的总模式损耗，作为波长的函数。

• (b) 三个最低损耗模式的近场分布，使用线性比例的伪彩色图表示。

• (c) 三个最低损耗模式的远场分布，使用线性比例的伪彩色图表示。

  
  

  我们现在考虑一个腔长为L = 2 mm的示例设备，该设备能够在连续波操作下实现数十瓦的功率输出【2,6】。对于该设备尺寸，我们实现了较高的外部效率，ηsubstrate = 0.94。

  在图8中，我们绘制了设备的模式光谱，以及三个最低损耗模式的近场和远场分布。可以看出，最低损耗模式具有非常窄的圆形远场分布，这在其他大面积PCSEL中也有类似表现【3,6】。这一模式对应于A带的最低损耗模式。

  次低损耗模式对应于A带的高阶腔体模式，这些模式的波长接近于基模，并具有窄的多峰场分布。在此L下，我们在两个最低损耗模式之间实现了模式区分度Δg = 2.6 cm⁻¹。

  

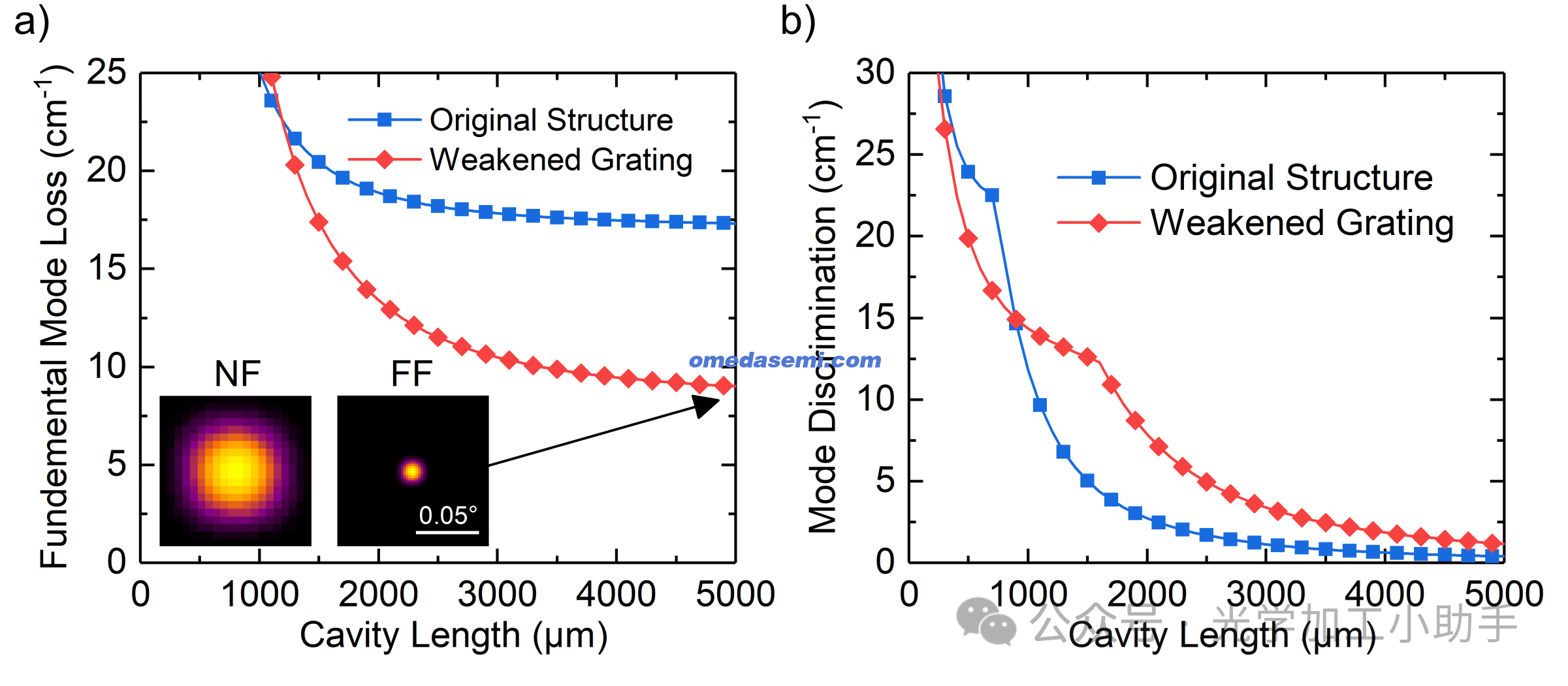
  图9. 改变原始设计的PCSEL（光子晶体表面发射激光器）以及一个具有弱化光子晶体光栅的PCSEL的腔长，并绘制：(a) g，最低损耗基模的总模式损耗（插图：腔长为5毫米时最低损耗模式的近场和远场分布，使用线性缩放的伪彩色图显示）；(b) ∆g，最低损耗基模与次低损耗模式之间的模式区分度。
  

  4. 讨论

  我们已经展示了在GaAs材料系统中设计全半导体PCSEL（光子晶体表面发射激光器）的可能性，其腔长范围为 L = 1–3 mm，具有较大的模式区分度、高外部效率以及窄的圆形远场分布。这是通过利用一种能够最小化 |κ₁D| 的光子晶体单元格设计实现的，该设计通过减少直接的一维耦合，同时保持高耦合效率和带边模式之间的区分。然而，要在实际设备中估算实现单模PCSEL所需的 ∆g 并不简单，因为其强烈依赖于温度、载流子以及本文未考虑的光学效应。

  先前研究表明，对于直径 D = 0.5 mm 和 D = 0.8 mm 的PCSEL，∆g ≈ 3–4 cm⁻¹ 可以实现高功率和窄远场操作【6】。最近的研究建议，对于直径 D = 3 mm 的PCSEL，模式区分度为 ∆g ≈ 0.5–1 cm⁻¹ 即足以支持单模操作【4】。在本文中，我们实现了 ∆g ≈ 1.1 cm⁻¹（腔长 L ≤ 3 mm），并且随着腔长减小，模式区分度更大。这表明我们全半导体设计适合高功率、高效率的单模或低模数操作。

  值得注意的是，这一结果是在单光子晶格设计下实现的，与先前研究中采用双光子晶格设计的方式不同。这表明我们的三角形单元格设计作为双晶格PCSEL的一种通用替代方案具有潜力。对于这类器件是否最终可制造的关键因素是设计对制造缺陷的适应性。初步模拟表明，我们的设计能够容忍如三角形角落圆化和结构尺寸小幅变化等潜在缺陷，这将在后续研究中进一步讨论。

  在先前关于高功率PCSEL的研究中，通过平衡总耦合矩阵 C 的一维和二维分量（分别由 κ₁D + iµeⁱθpc 和 κ₂D± 表示），可以实现更大的模式区分度【6】。这进一步降低了平面内光学约束，而不仅仅是减少 |κ₁D| 的幅值。然而，目前尚不清楚如何在全半导体设计中有效实现这一点，因为该设计需要较大的特征尺寸以实现强的垂直耦合，因此设计自由度比双光子晶格PCSEL更小。这是未来优化器件设计和扩大器件尺寸的一个潜在方向。

  另一种策略是通过减弱光子晶体的强度来进一步扩大器件尺寸，同时保持模式区分度。这可以通过减小光子晶体特征的高度，或者通过增加有源区与光子晶体之间层的厚度以减少光子晶体与垂直模式的重叠来实现。在图9中，我们将本文所讨论的原始结构与一种简单的减弱结构进行了比较。减弱结构中，光子晶体高度从 150 nm 减小至 100 nm，GaAs层的厚度从 50 nm 增加至 300 nm。减弱结构具有以下特性：无限腔垂直辐射损耗为 g = 8.6 cm⁻¹，模式区分度为 ∆g = 12.0 cm⁻¹，Hermitian耦合系数为 |κ₁D| = 21.7 cm⁻¹，|κ₂D+| = 9.6 cm⁻¹ 和 |κ₂D−| = 10.8 cm⁻¹。

  这种减弱结构在最大有限尺寸腔中实现了更大的模式区分度：当 L = 3 mm 时，∆g = 3.4 cm⁻¹；当 L = 5 mm 时，∆g = 1.2 cm⁻¹。在 L = 5 mm 时，最低损耗模式仍能维持大面积单峰近场分布和窄的圆形远场分布，尽管结构中二维耦合减弱。这表明，通过该方法，可以实现单模或低模数操作的全半导体PCSEL，其输出功率可达到数十瓦甚至数百瓦【4】。

  然而，减弱光栅的权衡在于PCSEL模式的表面损耗降低，这需要仔细最小化光学损耗以实现高效激光器（DP.1）。此外，减弱光栅还会降低带边模式之间的模式区分度（DP.2），可能导致多个带边模式同时激射，从而产生多个彼此接近的波长。

  5. 结论

  在本研究中，我们提出了一种基于InGaP/GaAs全半导体光子晶体的PCSEL（光子晶体表面发射激光器）设计，适用于超大发射面积和高功率操作。利用PCSEL的耦合波理论，我们对无限腔PCSEL进行了建模，展示了由拉伸并旋转的等腰三角形组成的单元格可以在以下方面表现出优异性能：

  在四个带边PCSEL模式之间提供较大的模式区分度；

  实现最低损耗模式的大耦合损耗；

  保持较小的一维耦合强度。

  我们认为这种特性是双晶格设计的有前途的通用替代方案。

  通过有限腔器件建模，我们展示了经过优化的PCSEL在 L = 1–3 mm 的大腔长下，可以实现与最佳的含空腔设计相当的模式区分度和外部效率。这是首次在全半导体PCSEL中实现这样的性能。我们还提出了实现更大器件（腔长达 L = 5 mm）的路径，为进一步扩大PCSEL设计规模和性能提供了依据。